++ 50 ++ 正六面体 展開図 のりしろ 133371-正六面体 展開図 のりしろ

50素晴らしいサイコロ 展開 図 のりしろ melan melani 年10月16日金曜日 サイコロの展開図 無料ダウンロード 印刷 幼児教材 知育プリント サイコロ展開図 のりしろ の無料イラスト素材 イラストイメージ ボード 勞作 のピン のりしろ付きサイコロ展開図4 確かに正十二面体の展開図になっていることを確認したら，再び『正五角形定規』を用い て，全くじ展開図をケント紙に写します。今度はできるだけ丁寧に描きましょう。 5 写した展開図を丁寧に切り抜いて，組み立てましょう。 トップ 100 正方形 展開 図 直方体の展開図 54通り 算数の広場 立方体の展開図 11種類 プリント ちびむすドリル 小学生 立方体の展開図11種の画期的な覚え方 問題の解き方を解説 数学fun 立方体の展開図 11種類 プリント ちびむすドリル 小学生 イメージが

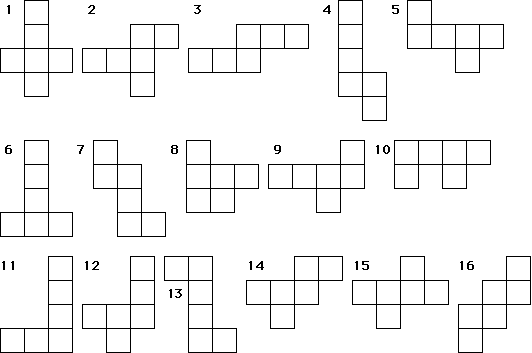
イメージが苦手でも解ける 立方体の展開図 算数の教え上手 学びの場 Com

正六面体 展開図 のりしろ

正六面体 展開図 のりしろ-せると、正八面体になる。のりしろがあるので、成形しやすい。 図5．正八面体の作り方（2) (4) 双三角錐 2つの正四面体を上下にくっつけると、双三角錐（デルタ六面体）になる。2つのものをくっ つければ作られるのは当然である。今回は，六方二十面体（ろっぽうにじゅうめんたい）＝The Hexakisicosahedronです。 これはアルキメデスの立体のうち，大菱形二十面十二面体>4,6,10の双対 変形立方体 Wikipedia 六面体 展開 図

多面体

（2） 右の図のような長方形 を、直線 hを軸として回転させ てできる立体の見取図を書き なさい。 例題5 右の図は立方体の展開図である。 この立方体を組み立てたとき、 次の問いに答えなさい。 （ 1） 辺abと垂直な面はどれか （ 2） 辺abと平行な面はどれか 問題 下の展開図をくみ立てた時に、辺あいに重なる辺 は作り方 画用紙を用意し、画用紙の端を利用してこのような展開図を書きます。 今回は、各辺3cmで作りました。という時に、サイコロだけ行方不明になっていてない！っていう事よくありますよね。 面体展開図の無料イラスト素材 イラストイメージ 正多面体の塗り分け ちょっと変わったn色問題 50 正十二面体 展開図 書き方 壁紙 配布 いろいろな立体の問題 切頂面体 もどき 展開図 ペーパークラフト 正多面体クラブ 正多面体は、正四面体、正六面体、正八面体、正12面体、正

 面体 展開 図Q ・12面体の展開図探してます。 宿題で・12面体を作成するという宿題が出ました。 そのため・12面体の展開図を探しています。 どなたかよろしくお願いします。Author 教育出版 Created Date 3/30/16 AMペーパー 切頂二十面体の展開図を作ってみました。 のりしろ付きのシンプルなサイコロ展開図をデザインした知育イラスト素材ですプリンターなどで紙にプリントしてご利用ください カテゴリ 知育サイコロ 商品id 9922 2510 133 サイコロ展開図 のりしろ の無料イラスト素材 イラストイメージ のりしろ付き キャラメル箱 パッケージ印刷展開図作成サービス ネット印刷は 印刷通販 グラフィック サイコロ 作り方 展開 図 サイコロ 作り方 展開 図サイコロの展開図。英語でダイス(dice)。 別名、賽（さい）。形だけならば立方体とか正六面体とも。

展開図で表される立体 六角錐 展開図で表される立体 正十二面体 展開図で表される立体（ただし、どの面もすべて合同な正多角形） 正四面体 展開図で表される立体（ただし、どの面もすべて合同な正多角形） 正六面体 展開図で表される立体（ただし 寸法：10㎝ × 10㎝ × 10㎝ (のりしろは含まない、のりしろ幅1㎝) この立方体の展開図を元に、以下の2つの方面からアプローチしていきます。 ・角をアレンジする ・辺をアレンジする立方体展開図ハンコ (のりしろ付き) お買い物の前に必ず minneお客様規約 をご確認くだ 立方体展開図 のりしろ付きの全11パターン 無料でダウンロード 3ステップでわかる 立方体 正六面体 の展開図の書き方 解き方

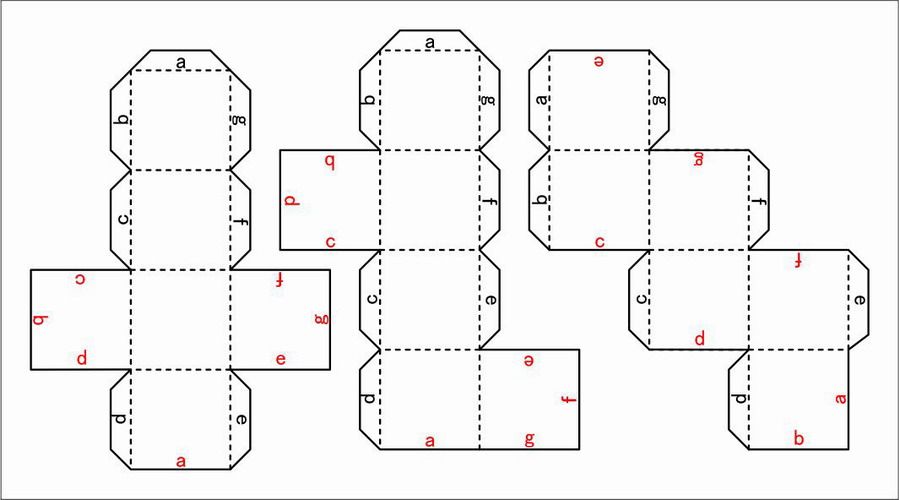
ローカルペーパークラフト エバンゲリオン 2 Araさんのブログ 楽天ブログ

用紙作成 表紙作成や統計地図も 用紙作成を強力サポート 花子21 ジャストシステム

のりしろ① ③ ② ③ ② ② ③ ③ 立方体ブロック展開図 1 ． は じ め に 外 側 の 線 に 沿 っ て 切 り 取 り ま す 。 2 ． 折 り 目 を つ け ま す 。 赤 い 線 は 谷 折 り 、 黒 線 は 山 折 り で す 。 3 ． の り し ろ ① に 糊 を つ け て 筒 状 を 作 り ま す 展開図を印刷して組み立てることで、幾何模型を手に取って触れることができるようになります。 切頂面体 ダウンロードtruncated_polygonszip (30KB) (上記一式の展開図データがzip形式で圧縮してあります)正多面体の展開図は正四面体で2種類、正六面体で11種類、正八面体で11種類、 正十二面体で種類石倉塾特製 正多面体の展開図② 正六面体の展開図 やまおりせん のりしろ ていねいにきりぬいて くみたててみよう！

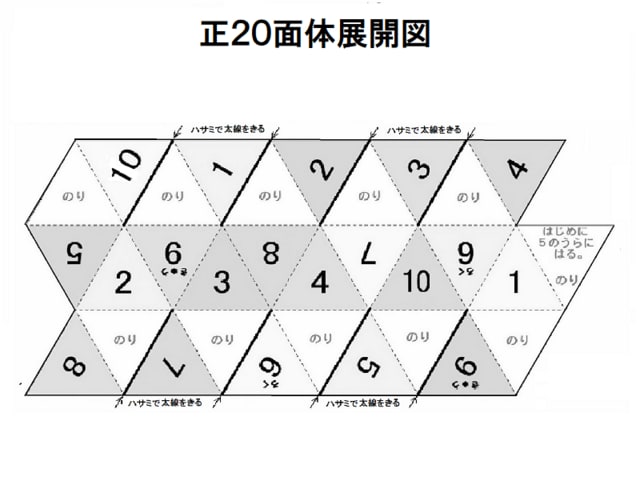
サイコロを作ろう 正二十面体 作って遊ぼう 社会に開かれた学校の応援

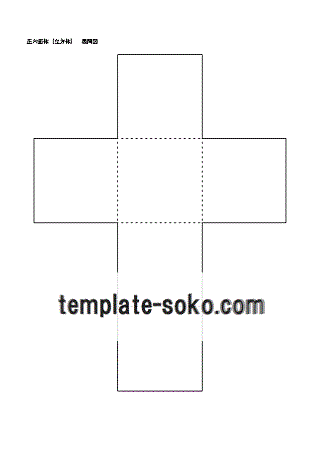
展開図 正六面体 Word作成のテンプレートを無料ダウンロード

 立方体展開図 のりしろ付きの全11パターン 無料でダウンロード 無料のテンプレート サイコロ 正六面体の展開図 工作用紙でサイコロの展開図を作ってみた 爆走おてうブログ 25展開図になるための制約条件(2) 「切る」辺がサイクルを持たない = ￢( 「切る」辺がサイクルを持つ) サイクルの列挙 fサイクルの集合= 0 foreach 面( xi1, xi2, xi3, xi4) { f1= xi1∧xi2∧xi3∧xi4 ∧他変数の負リテラル f2= fサイクルの集合のBDDで、 xi1, xi2, xi3, xi4 のの 00枝枝 とと 11枝枝 をを 入入 れれ図版ワークシート集 ご覧になる前にお読みください。 このページは，画面の幅が1024px以上の，パソコン・タブレット等のデバイスに最適化して作成しています。 スマートフォン等ではご覧いただきにくい場合がありますので，あらかじめご了承ください

完了しました 立方体 の 展開 図 ニスヌーピー 壁紙

次の立体の展開図を組み立てたとき 正しいものはどれか この問題の簡単な考 Yahoo 知恵袋

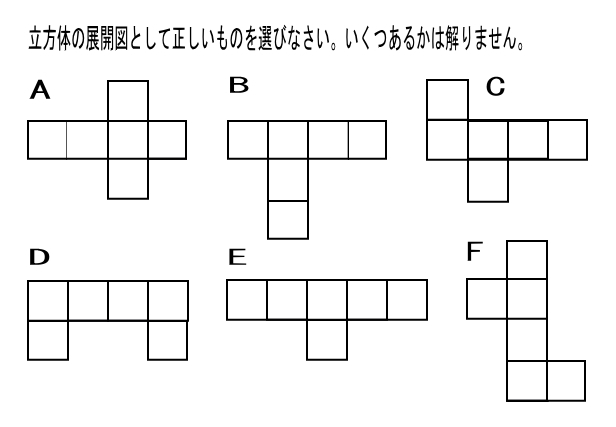
100 箱ひげ図の考案者とヒンジ 13年6月 99 標準偏差が整数のデータ 13年6月 98 風呂敷と「1次変換」 13年5月 97 四分位数の誕生と考案者 13年5月 96 数列の質問 13年4月 95 階差数列 13年4月 94 長さが計算可能な曲線 13年3月 93 データの分析のオリジナル問題それぞれの名前は左から、 『正四面体』『正六面体（立方体）』『正八面体』『正十二面体』『正二十面体』 です。 正多面体の性質 正多面体の問題では、面の形・面の数・頂点の数・辺の数などが問われます。 これらを表にまとめると次の通り。 正面体 の場合 ① 1色 問題を考えるにあたって実際に「見て確かめる」ために正面体を作ってみたので，その展開図を"おまけ"としてつけておきます．ご利用いただければ幸いです． おまけ～正面体は，正六面体(立方体)のみである。第4学年で， 立方体，直方体について学習する。ここ

多面体

3ステップでわかる 立方体 正六面体 の展開図の書き方 解き方 Qikeru 学びを楽しくわかりやすく

 多面体 展開 図 ダウンロード ペーパークラフトを作ろう 展開図のダウンロード 多面体の等分 Divided Polyhedron;正多面体の展開図データ作成を別プログラムとした Ver12 07/12 準正多面体、正多角柱、正多角反柱、正多角錐、デルタ多面体などを追加 Ver13 09/07 展開図の一部変更 （正4面体, 立方体, 正8展開図が1−4−1型なので、どの点が接するか考えるのは難しくありません。 展開図の周の長さは、どれも同じだ！そして、辺の数にすれば14辺分だ！ 展開図でつながっている箇所の数は、どれも5か所だ！ 何故、そんな一致点があるのでしょうね？ サイコロの展開図と作り方/ 無料ダウンロード・印刷 サイコロの展開図。 英語でダイス (dice)と言い、 別名、賽（さい）。 形だけならば立方体とか正六面体ともいわれます。 無料でダウンロードできるシートを使ってサイコロを作っていきます。 目次

多面体

エレガント立方体 展開 図 のりしろ 子供のための最高のぬりえ

PLATEX kousakukurabu /1/30(928) 229 第1章「のりを使わない正十二面体・正二十面体の展開図」 33C 32D 26A 12B 11A 22C 33A 32B 31C 33D 24A 13B 12A 23B 31A 33B正多面体は、正四面体、正六面体、正八面体、正12面体、正面体の5種類しかない。 正四面体と立方体は簡単にできる。 これをもとに、他の立体を作図してみよう。 まずネットでそれぞれの多面体を調べてみよう。 どう作図できるか浮かんでくる。 展開図を印刷して組み立てることで、幾何模型を手に取って触れることができるようになります。 ここで公開しているデータは、どなた様も 無料 でダウンロードしていただけます。 教育用途などでご活用いただければ幸いです。 正二十面体 Wikiwand 面体

完了しました 立方体 の 展開 図 ニスヌーピー 壁紙

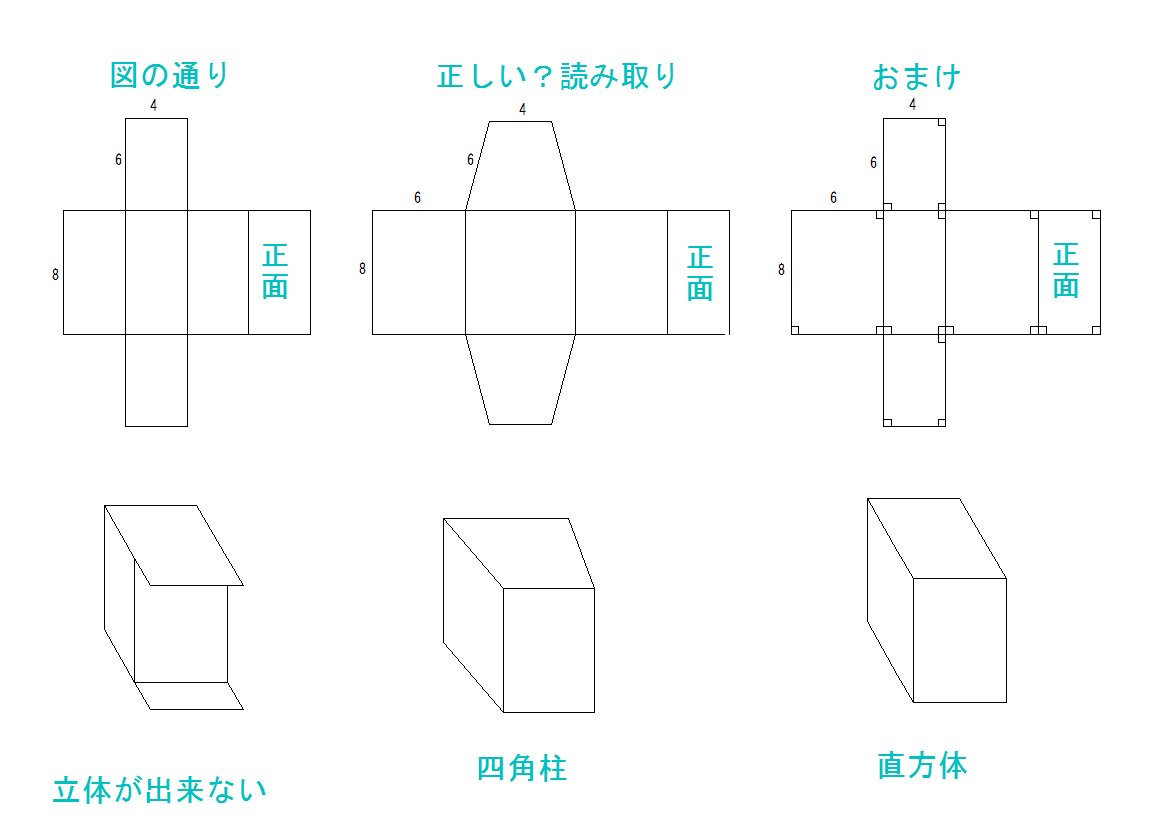
この小学生の算数の問題成り立ってる 展開図の解答をめぐって大人も大紛糾 Togetter

Title rippotai_tenkaizu01 Created Date PM展開図とそこから折れる凸立体の研究 1複数の箱が折れる共通の展開図 •2通りの箱が折れる共通の展開図 •3通りの箱が折れる共通の展開図 そして残された未解決問題たち 2正多面体の共通の展開図 3正多面体に近い立体と正4面体の共通の展開図(予備1展開図の基礎的な知識 1正多面体の共通の展開図 2複数の箱が折れる共通の展開図：2時間目 3RepCube：最新の話題 4正多面体に近い立体と正4面体の共通の展開図 5ペタル型の紙で折るピラミッド型：2時間目～3時間目

07 2233号 展開図画像作成装置および方法並びにプログラム Astamuse

立体展開図プリント無料ダウンロード 空間把握にお役立ち工作 頭がいい子に育てる知育玩具と学習方法

Title 正多面体 Created Date AM

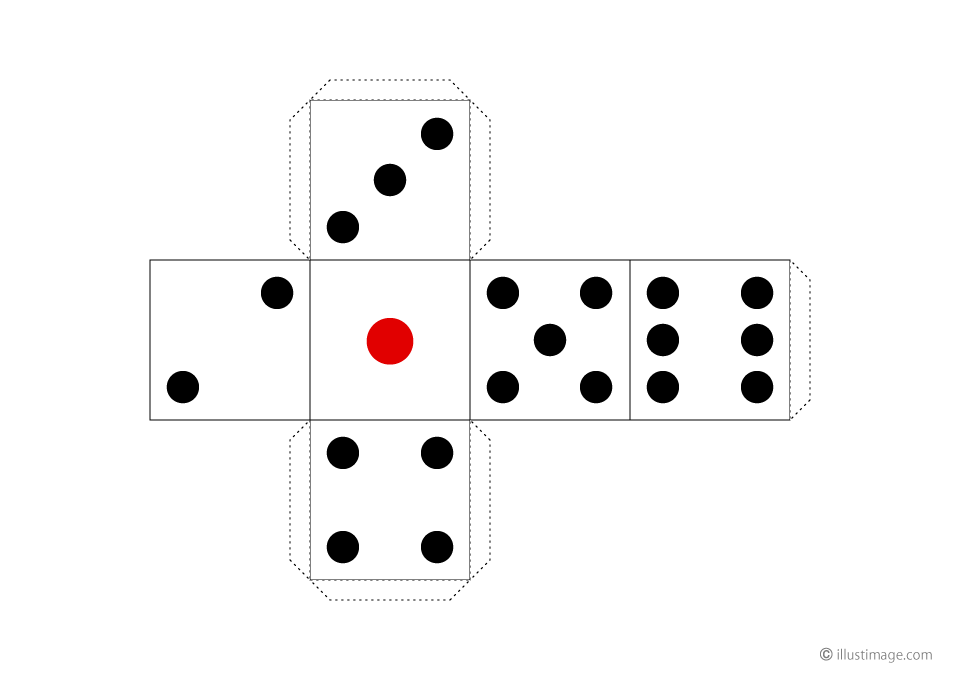
サイコロ展開図 のりしろ イラストのフリー素材 イラストイメージ

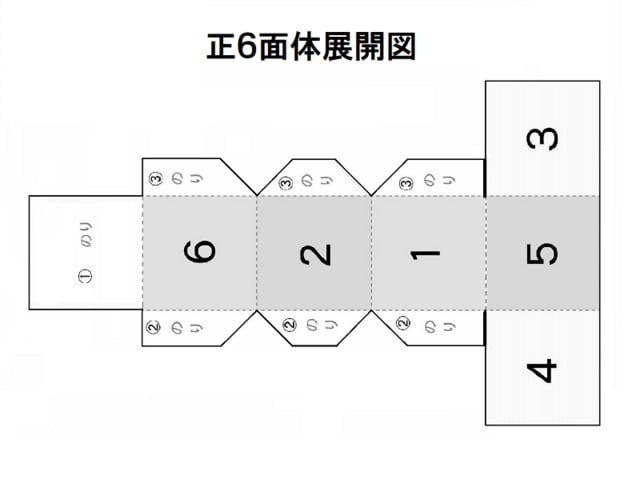
サイコロを作ろう 正六面体 作って遊ぼう 社会に開かれた学校の応援

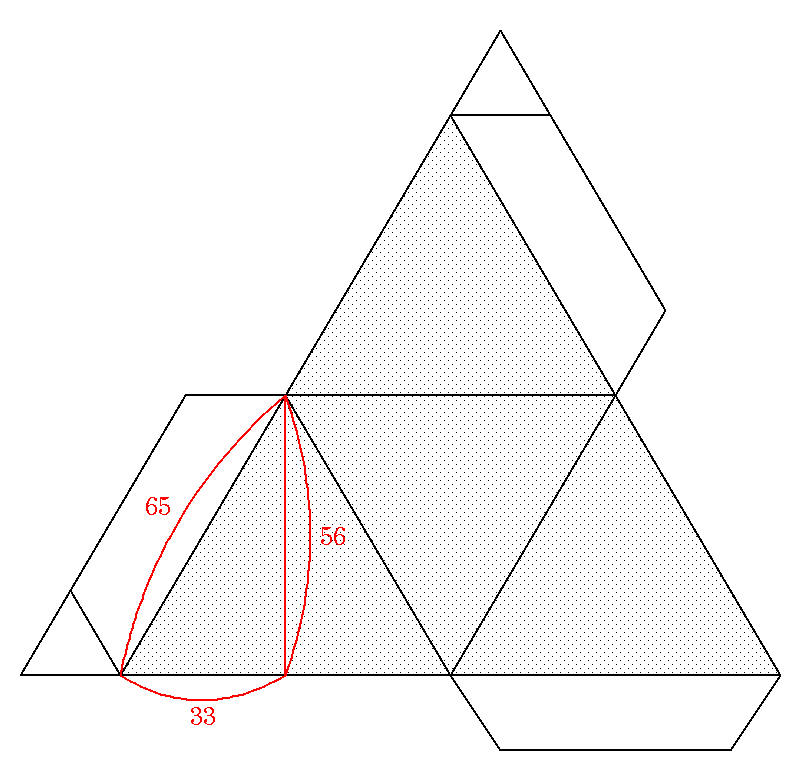
いろいろ のりしろ 付き サイコロ 展開 図 シモネタ

サイコロを作ろう 正十二面体ｂ 作って遊ぼう 社会に開かれた学校の応援

イメージが苦手でも解ける 立方体の展開図 算数の教え上手 学びの場 Com

正面体ペーパークラフト 展開図 正多面体クラブ

展開図

多面体

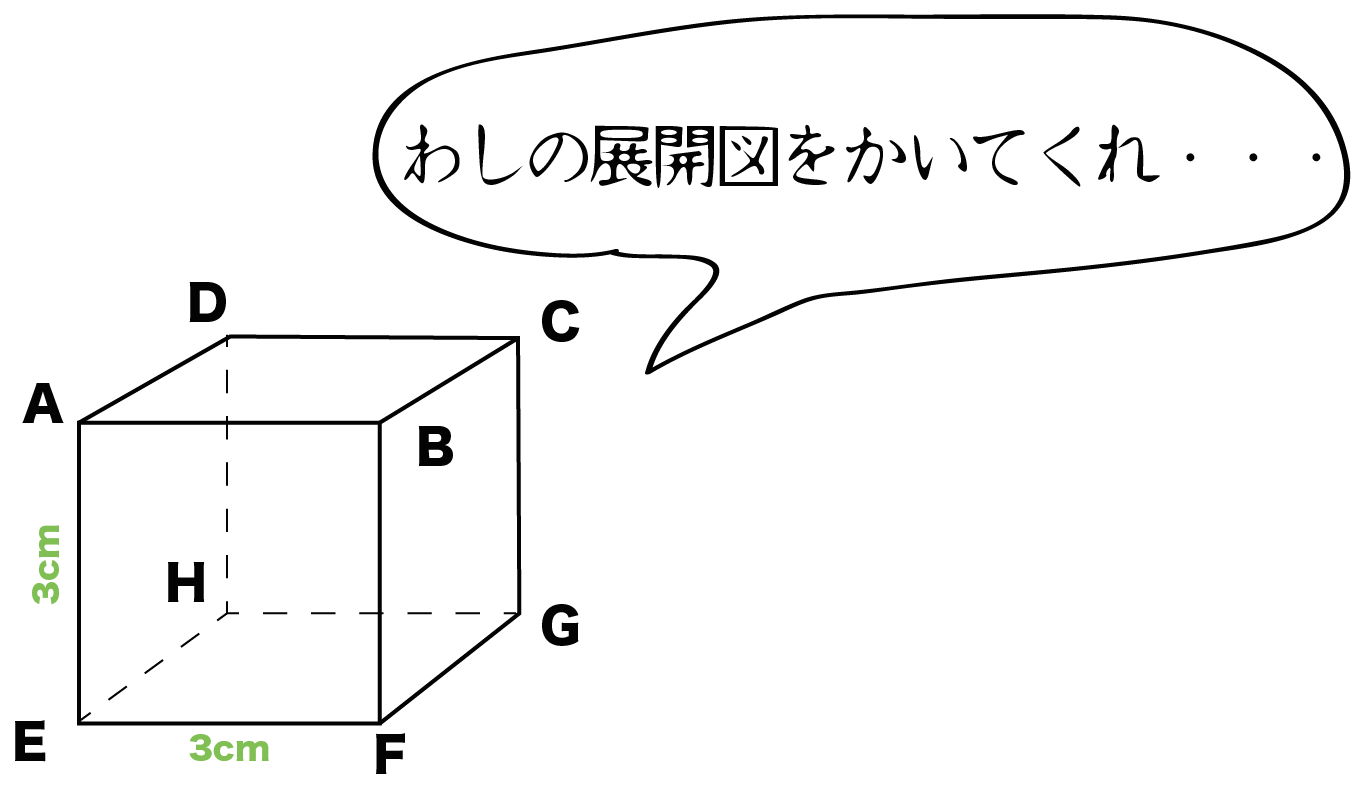
3ステップでわかる 立方体 正六面体 の展開図の書き方 解き方 Qikeru 学びを楽しくわかりやすく

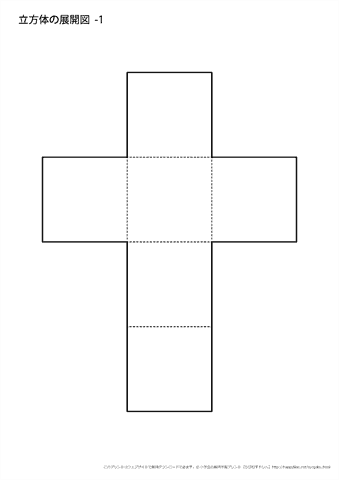
立方体の展開図 11種類 プリント ちびむすドリル 小学生

正多面体

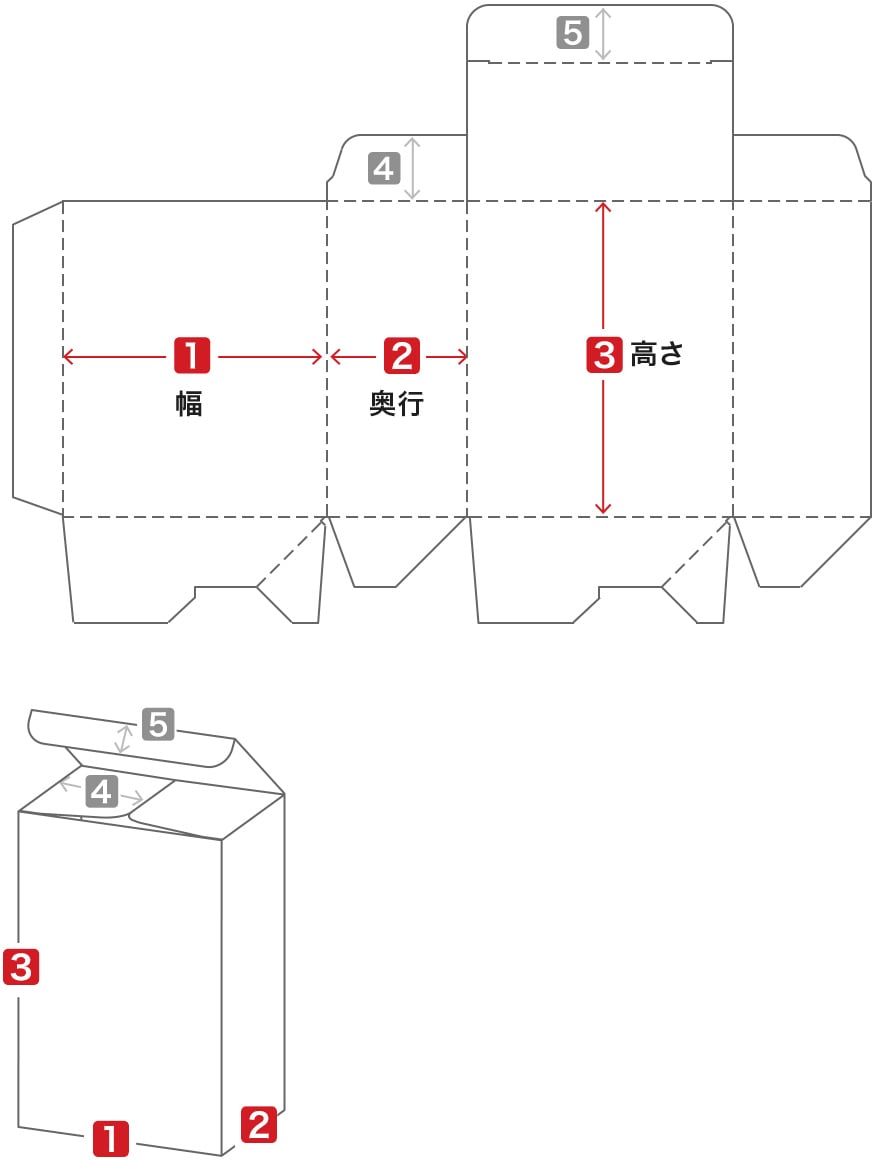
ワンタッチ底 パッケージ印刷展開図作成サービス ネット印刷は 印刷通販 グラフィック

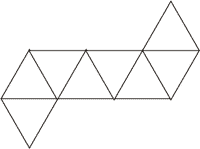
展開図

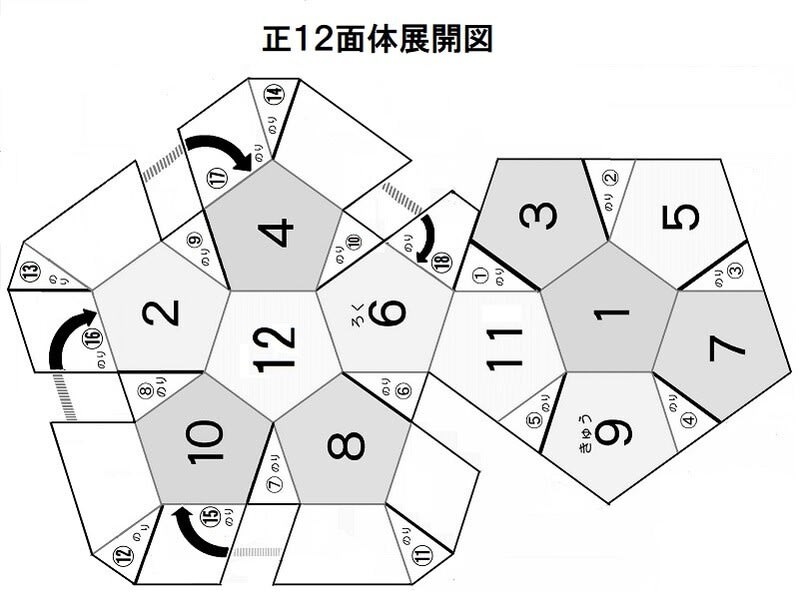
年9月のブログ記事一覧 作って遊ぼう 社会に開かれた学校の応援

メルカリ 正多面体展開図 参考書 1 080 中古や未使用のフリマ

菱形12面体ペーパークラフト展開図 正多面体クラブ

立方体の展開図の分割

サイコロ展開図 のりしろ イラストのフリー素材 イラストイメージ

エレガント立方体 展開 図 のりしろ 子供のための最高のぬりえ

エレガント立方体 展開 図 のりしろ 子供のための最高のぬりえ

正六面体の展開図 Nano25の数学学習ソフトウェア

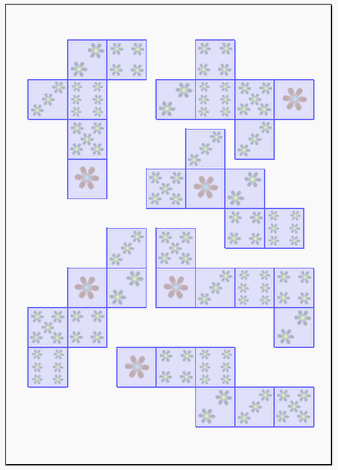
無料のテンプレート サイコロ 正六面体の展開図

正立方体の展開図について 皆様 こんにちは 来週から Yahoo 知恵袋

Zoids Ignition ゾイドイグニッション

1

立方体展開図ハンコ のりしろ付き はんこ スタンプ 鼠の王国製作所 通販 Creema クリーマ ハンドメイド 手作り クラフト作品の販売サイト

立体展開図プリント無料ダウンロード 空間把握にお役立ち工作 頭がいい子に育てる知育玩具と学習方法

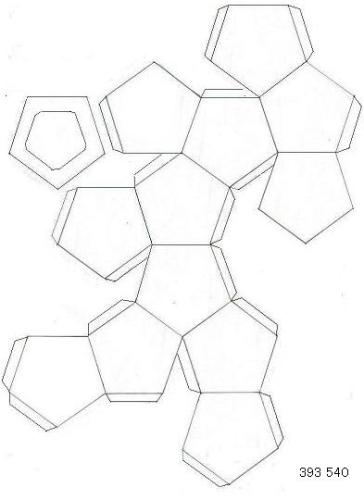
10年08月10日の記事 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ

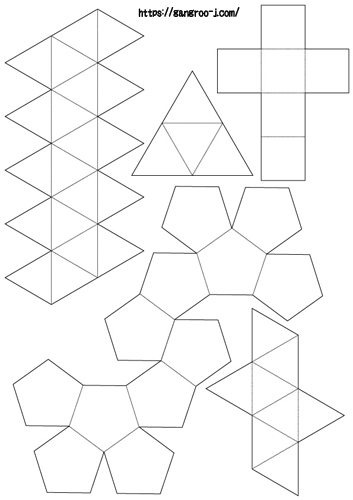
立体展開図プリント無料ダウンロード 空間把握にお役立ち工作 頭がいい子に育てる知育玩具と学習方法

立方体の展開図の分割

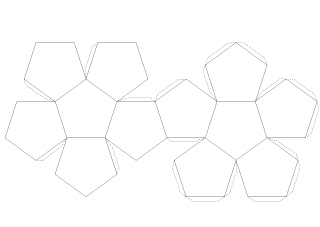
サイコロ展開図 のりしろ イラストのフリー素材 イラストイメージ

エレガント立方体 展開 図 のりしろ 子供のための最高のぬりえ

基本的な展開図の作成

1

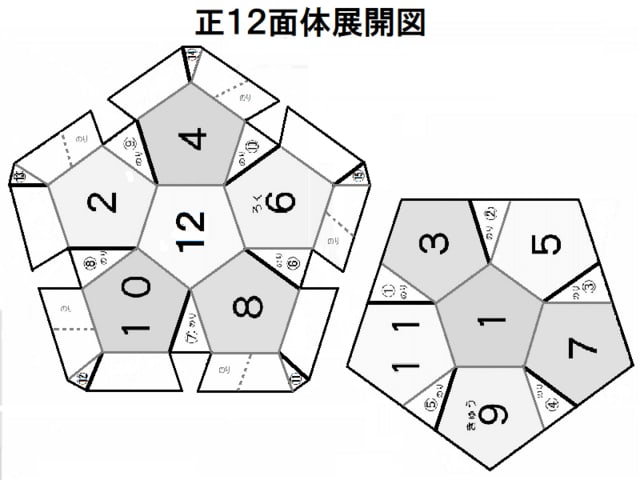
サイコロを作ろう 正十二面体ｃ 作って遊ぼう 社会に開かれた学校の応援

正多面体

正六面体の展開図 Nano25の数学学習ソフトウェア

1

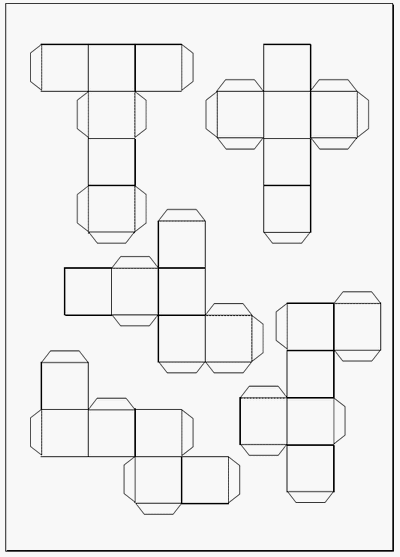
立方体展開図 のりしろ付きの全11パターン 無料でダウンロードできるフォーマット テンプレート 雛形

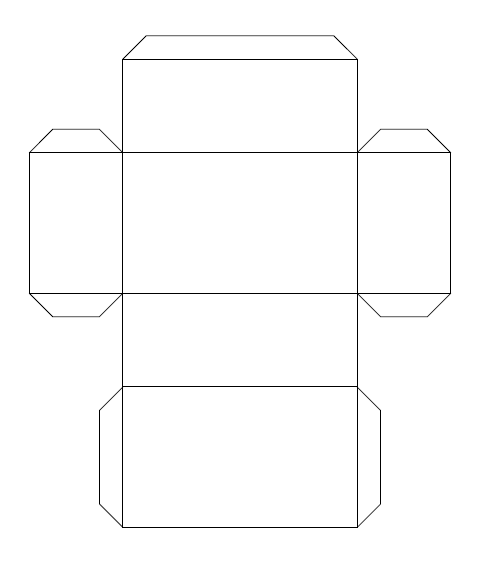
直方体展開図の作成

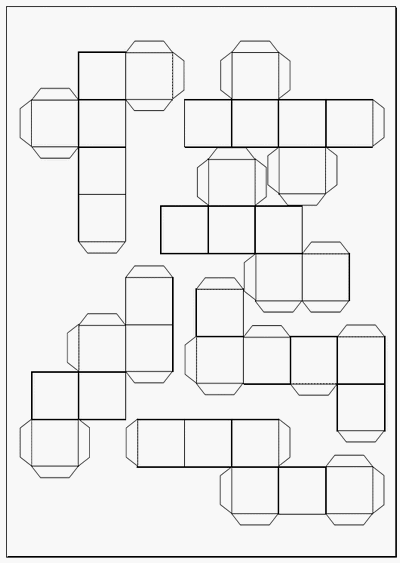
立方体展開図 のりしろ付きの全11パターン 無料でダウンロードできるフォーマット テンプレート 雛形

立方体の展開図11種の画期的な覚え方 問題の解き方を解説 数学fun

正多面体ペーパークラフト 正多面体クラブ

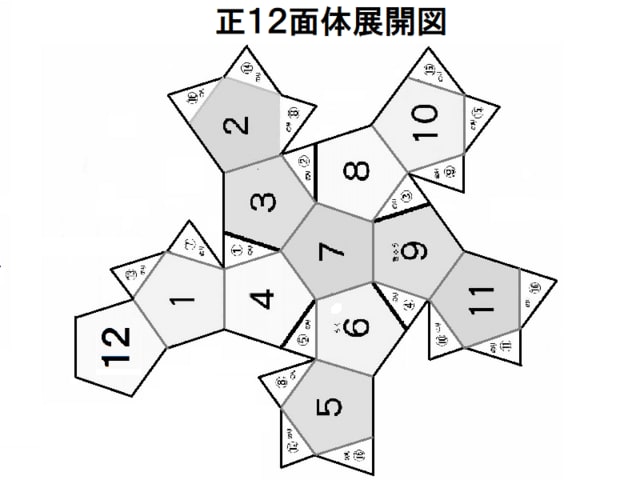
サイコロを作ろう 正十二面体ａ 作って遊ぼう 社会に開かれた学校の応援

ペパクラデザイナー 幾何模型のダウンロード

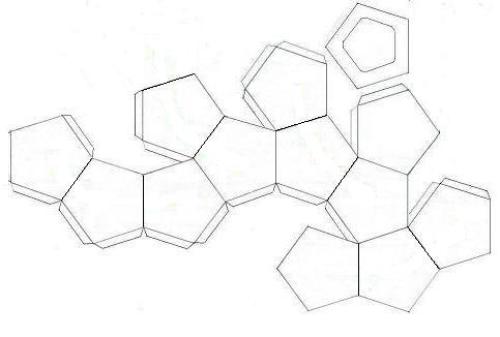
3ページ目の 数学 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ

Japan Image サイコロ 展開図 のりしろ

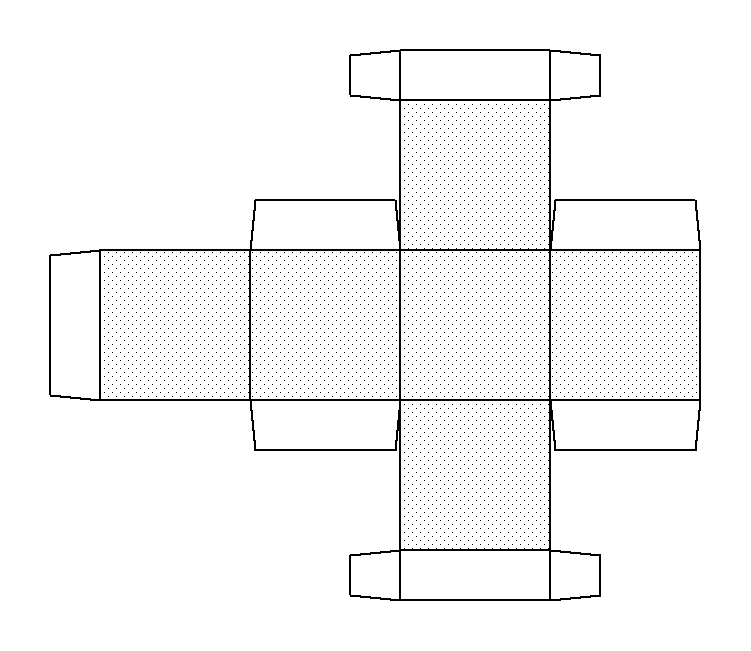
基本的な展開図の作成

無料でダウンロード 直方体 展開 図 パターン ニスヌーピー 壁紙

正多面体 準正多面体の展開図

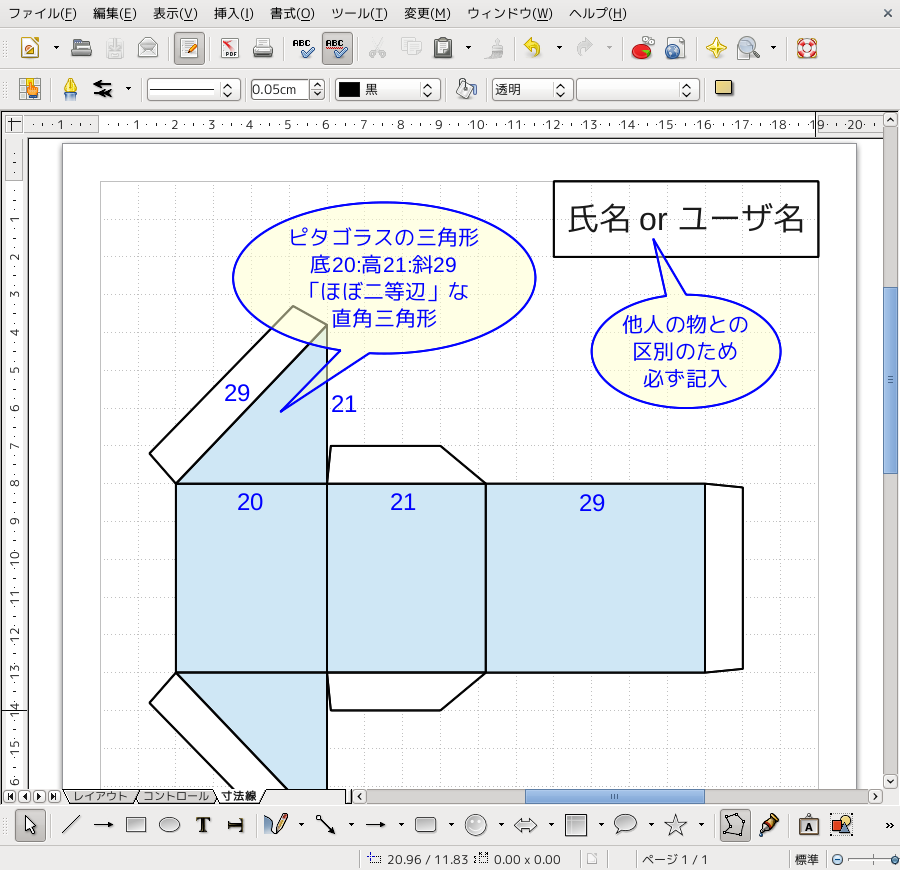
基本的な展開図の作成

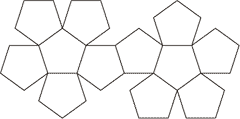
展開図

正面体ペーパークラフト 展開図 正多面体クラブ

機械設計のための基礎製図

Q Tbn And9gcqiuepwujk7m1rhdahp 87vxpzzlpra7dgu7s2wrmhlvk75uaz1 Usqp Cau

サイコロ展開図 のりしろ イラストのフリー素材 イラストイメージ

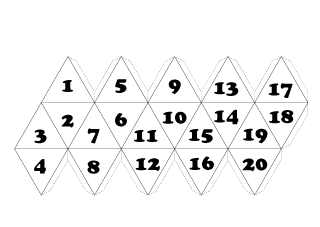
サイコロ展開図 のりしろ イラストのフリー素材 イラストイメージ

多面体

最高 Ever サイコロ 展開 図 のりしろ

ペパクラデザイナー 幾何模型のダウンロード

菱形12面体ペーパークラフト展開図 正多面体クラブ

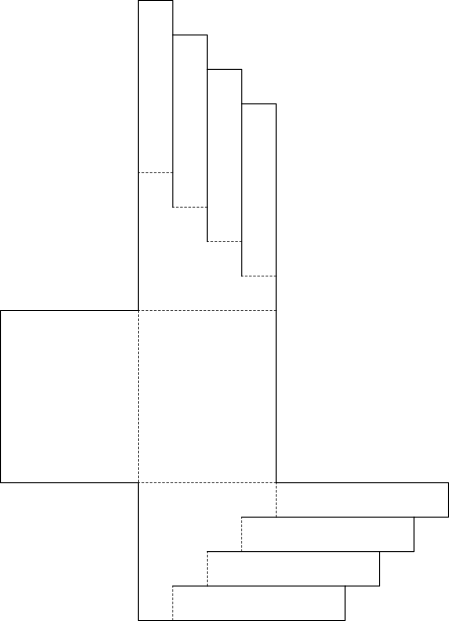
いろいろな立体の見取図 展開図 体積 表面積 算数の広場

基本的な展開図の作成

立方体の切断 模型の原紙を頒布します 駒澤塾 中学受験の算数 理科

正六面体の展開図のイラスト素材

正面体ペーパークラフト 展開図 正多面体クラブ

立体制作 Rio Ueda

多面体

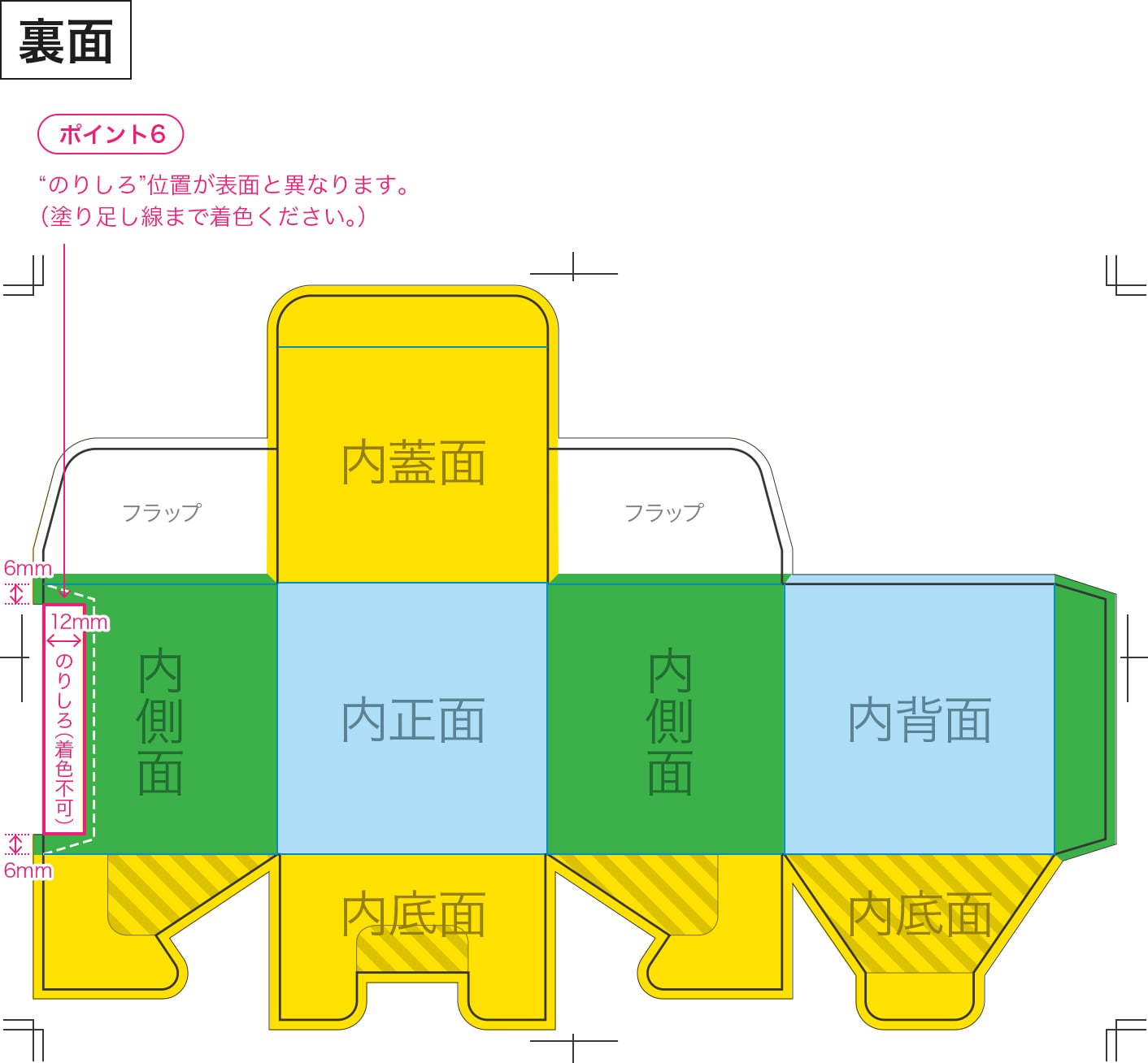
エレガント立方体 展開 図 のりしろ 子供のための最高のぬりえ

サイコロ展開図 のりしろ イラストのフリー素材 イラストイメージ

立方体展開図ハンコ のりしろ付き ハンドメイドマーケット Minne

1995 0294号 ３２面体の地球儀用材料 および その製作方法 Astamuse

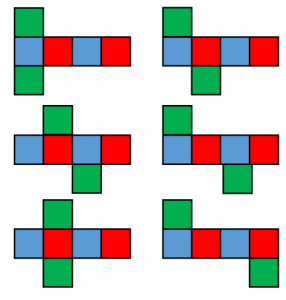
立方体の展開図の一覧および面や辺の対応 具体例で学ぶ数学

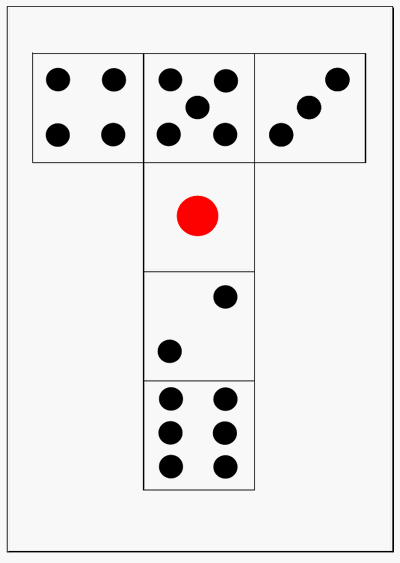
さいころ展開図 のりしろ付きもあります 雛形の無料ダウンロード

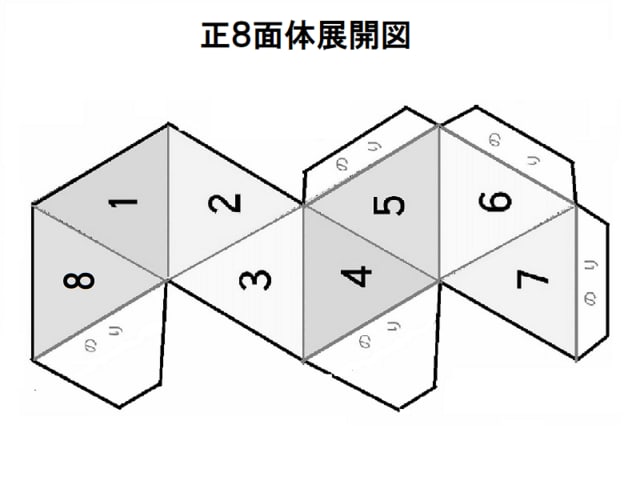
サイコロを作ろう 正八面体 作って遊ぼう 社会に開かれた学校の応援

トップ 100 サイコロ 作り方 展開 図

正面体ペーパークラフト 展開図 正多面体クラブ

立方体の展開図 11種類 プリント ちびむすドリル 小学生

新着記事一覧 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ

3ステップでわかる 立方体 正六面体 の展開図の書き方 解き方 Qikeru 学びを楽しくわかりやすく

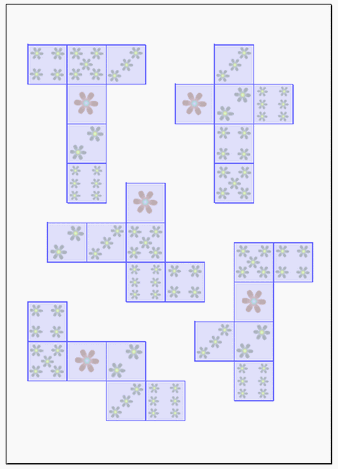
無料のテンプレート サイコロ 正六面体の展開図

正六面体の展開図のイラスト素材

ペパクラデザイナー 幾何模型のダウンロード

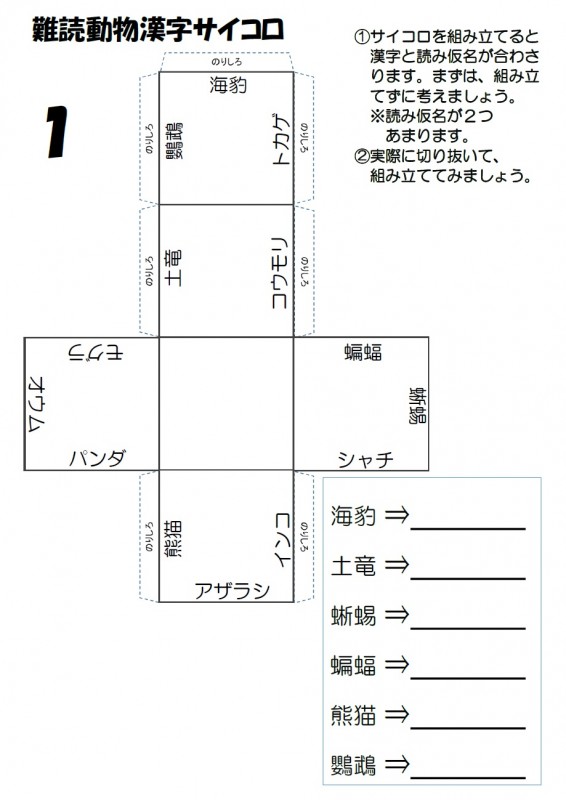
最新情報 北新宿第二地域交流館 福祉 介護 支援 社会福祉法人 奉優会 ほうゆうかい

多面体

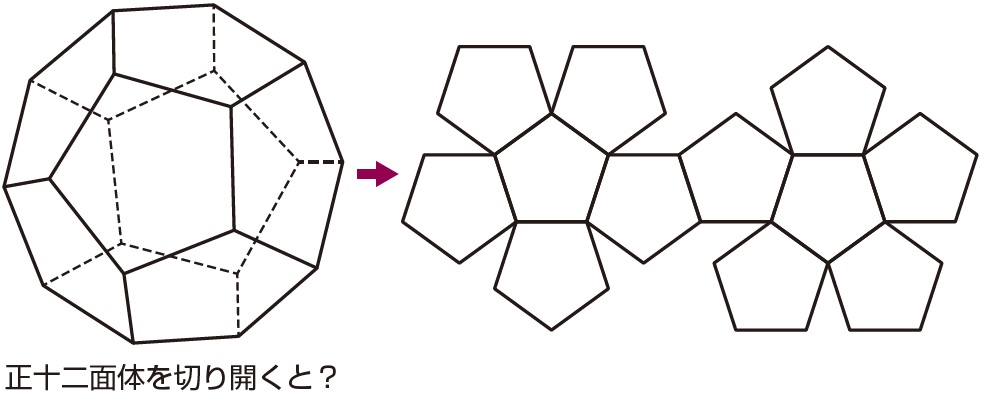
立方体の展開図は何種類ある 難関中学の受験に役立つ基礎知識 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン

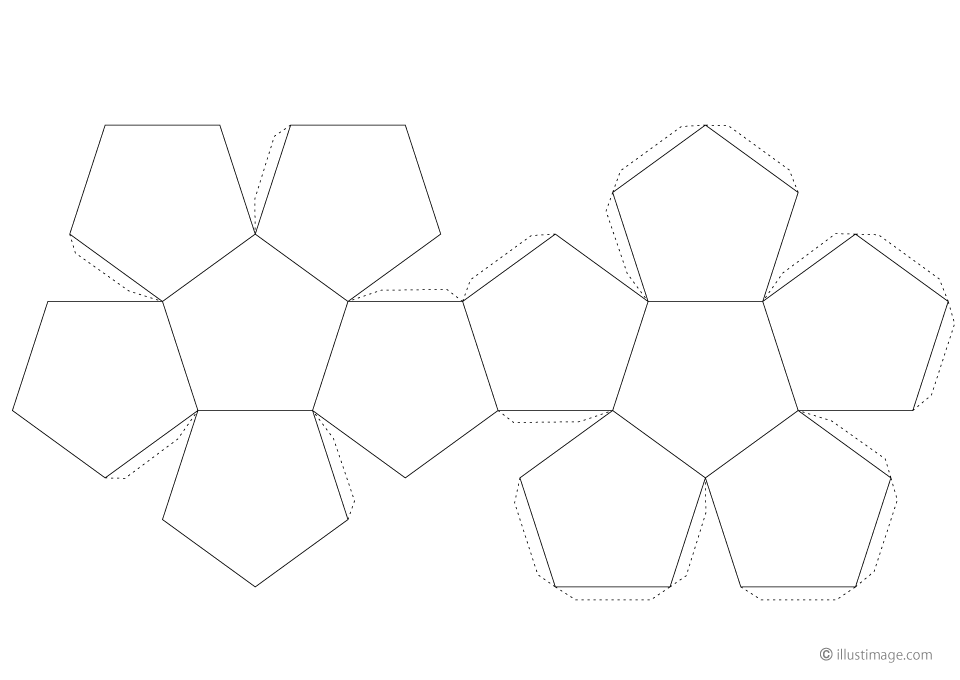
12面体展開図イラストのフリー素材 イラストイメージ

正多面体

立方体展開図ハンコ のりしろ付き Nmci In

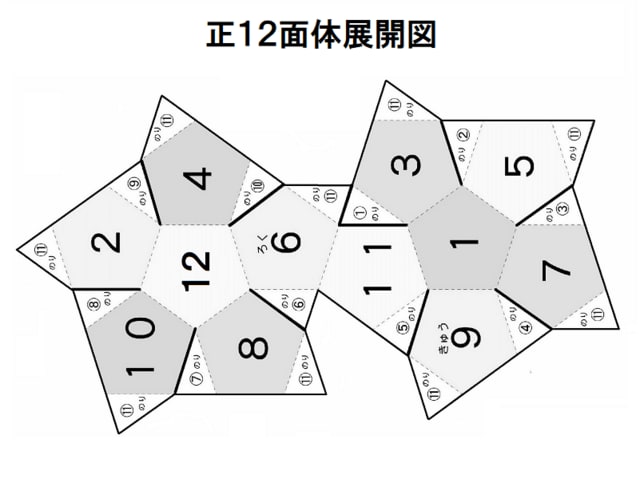
サイコロを作ろう 正十二面体ｂ 作って遊ぼう 社会に開かれた学校の応援

Incoming Term: 正六面体 展開図 のりしろ,